|
|
 |
|
Calanoida ( Order ) |
|
|
|
Clausocalanoidea ( Superfamily ) |
|
|
| |
| | | |
| Tharybidae Sars, 1902 ( Clausocalanoidea ) | | Ref.: | Sars, 1902 (1903) (p.66); Gurney, 1931 a (p.85); Rose, 1933 a (p.164); Brodsky, 1950 (1967) (p.83, 275); Vervoort, 1957 (p.96, Rem.); Fleminger, 1957 a (p.347, 349: Genera Key.); Tanaka, 1960 a (p.126); Bradford, 1969 b (p.502, Table 3); Andronov, 1974 a (p.1005); Schulz, 1981 (p.169); Bowman & Abele, 1982 (p.9); Razouls, 1982 (p.380); 1993 (p.311); Brodsky & al., 1983 (p.144, 147); Bradford & al., 1983 (p.123, Def.); Huys & Boxshall, 1991 (p.419); Chihara & Murano, 1997 (p.920); Bradford-Grieve & al., 1999 (p.881, 903, 904, 934); Ohtsuka & Huys, 2001 (p.461); Boxshall & Halsey, 2004 (p.12, 15; 209: Def., key of Genera, Rem.); Ferrari & Markhaseva, 2005 (p.45, Rem.); Vives & Shmeleva, 2007 (p.857, part. Key G.); Blanco-Bercial & al., 2011 (p.103, Table 1, Fig.2, 3, 4, Biol. mol, phylogeny); Markhaseva & al., 2014 (p.63, 67, 79, Table 1, 2, 3, 4, Def. Rem.: p.81); Laakmann & al., 2019 (p.330, Table 1, fig. 1, 2, 3, 4, Table A, phylogenetic relationships)
Bradford-Grieve J.M., (2002 onwards). Key to calanoid copepod families. Version 1 : 2 oct 2002. http://www.crustacea.net/crustace/calanoida/index.htm  | | Rem.: | On the occasion of the description of a new genus Parundinella, Fleminger (1957) reviews the taxonomic status of the family Tharybidae, included in the Isokerandria by Sars (1902). The author thinks that this family places itself naturally in the superfamily Paracalanina of Gurney (1931) and believes that the section, established by Sars is inadequate. Considering the relation between the genera, the author concludes that Pseudotharybis should be removed from this family, and notes the analogies with the genus Drepanopsis.
Undinella primitively included among the Scolecitrichidae has been removed from it by Brodsky (1950) who places it in the Tharybidae family.
The position of Bradford (1973, p.147) concerning certain genera and removed forms from the Phaennidae and the Scolecitrichidae, as well as the relations between the four families constituting the superfamily Paracalanidae is not clearly affirmed. She suggests either the creation of new families, or a grouping of all the Paracalanina comprising also the very distant Paracalanidae from the others. The families should be placed in the superfamily Pseudocalanoidea, the most evolved, arguing about the fact that taking into account the irreversibility of the evolutive mechanisms, the taxa that have lost some character descend from taxa having conserved them or of a common ancester.
For previous authors the family comprises 6 genera: Parundinella Fleminger, 1957; Tharybis Sars, 1902; Undinella Sars, 1900, to which we may tampt to add Pseudophaenna Sars, 1902; Neoscolecithrix Canu, 1896; and probably Parascaphocalanus Brodsky, 1955. The following species could be removed from the Scolecitrichidae and Phaennidae (Bradford, 1973) and included in the Tharybidae: Scolecithricella neptuni , Xanthocalanus paraincertus , X. hispidus , X. macrocephalon , X. paululus , Amallothrix robustipes , Amallothrix sp . Roe,1975. If Neoscolecithrix harmonises well with the characters defining the family, Pseudophaenna limits its precision and Tharybis and Undinella are difficult to separate. Schulz & Beckmann (1995, p.199) add the new genus Rythabis.
Vyshkvartzeva, 1999 (2000) (p.217-218) considers the genus Neoscolecithrix as belonging to the Scolecitrichidae family ('N.' antarctica, 'N.' farrani, 'N.' watersae).
Bradford-Grieve (2001) creates the genus Cenognatha with as type species Neoscolecithrix antarctica.
Andronov (2002, p.2) notices that the genera placed in this family are questionable.
Ohtsuka, Boxshall & Fosshagen (2003, p.61-62) judge that the family (sensu stricto) incorporates only three genera: Parundinella, Tharybis, Undinella; the case of Pseudophaenna remains uncertain in this family, the other genera (*), included in this family by various authors, should be considered as closer to the Scolecitrichidae (paraphyletic). Boxshall & Halsey (2004 (p.96) believe that the genus Pseudophaenna should be transferred to the Diaxidae family.
3 genera (+ 5 species incertae sedis).
The types of setae on the ramus of Mx2 include this family in the 'Bradfordian' group of families.
For Markhaseva, Laakmann & Renz (2014, p.81) 3 genera are included in the family; of them, only Tharybis Sars, 1902 is considered to be a true tharybid, but Undinella Sars, 1900 and Brodskius Markhaseva & Ferrari, 2005, conventionally currently remain in the family but are not considered for the family diagnosis. Schulz & Beckman (1995) assigned Rythabis and Pseudophaenna to the familly. Pseudophaenna was earlier tentatively placed in the family by Bradford & al. (1983). However, the placement of Pseudophaenna, Rythabis and Parundinella in the Tharybidae is doubful as their morphology differs in many details from that of Tharybis. They are neither closely related to Tharybis nor to each other, and must be placed outside Tharybidae and their status remains taxonomically unresolved.
Diagnosis after Markhaseva & al. (2003, p.17) based mainly on the characters of Tharybis; an apomorphy for the family is , apperently, the enlarged and vaulted Mx1 praecoxal arthrite :
- Proximal part of right A1 in males with ancestral segments X to XII fused (Fig.5).
- A2 coxa with or without seta; basis with 2 setae, endopod segment 1 with 2 setae; setal formula of exopod 0, 0-0-0, 1, 1, 1, 1, 1, 3 (Table 1).
- Md endopod segment 2 with 9 setae; exopod 5-segmented with 6 setae; gnathobase without hump/crest (Table 2).
- Mx1 setal formula 13-14, 2-3,3-4,2-3, 7 or 9, 3-5, 7 or 9 (Table 3).
- Mx2 endites formula 4, 3, 3, 3, 4; endopod setal formula 3 worm-like (W) + 5 brush-like (br), 3 worm-like + 6 brush-like, and 3 worm-like . 5 brush-like + 1 small sclerotized (sc) setae (Table 4).
- Mxp: praecoxal endites setal formula 1, 2 and 3, with all setae sclerotized, or 1sc+2sc+ (2sc+1w); 1sc+2sc+ (2sc+1br); 1w+ (1sc+1w)+(2sc+1w), and 1w+ (1sc+1w)+(2sc+1br); basis with 3 proximal and 2 distal setae (Table 5).
- Male P5 right basipod large; P5 left biramous, right uniramous, of complex structure (segments of irregular shape); right and left coxa and basis asymmetrical, right significantly shorter than left; right exopod 2-segmented, left 3-segmented (fig.7h)
For Markhaseva, Laakmann & Renz (2013, p.21) the precise differentiation between Diaixidae and Tharybidae is uncertain, and is based mostly on the enlarged and vaulted praecoxal arthrite of the Tharybis maxillule, which is, as proposed by Ferrari & Markhaseva, 2005, probable an autapomorphy of Tharybis (ca. a derived character unique to a given species or other monophyletic taxon).
For Laakmann & al. (p.330, Table 1; considered as incertae sedis gebera in the ''Bradfordian'' families (see Markhaseva & Ferrari, 2005; Markhaseva & al., 2014).
Total 3 G: Tharybis (Sars, 1902), Undinella (Sars, 1900), Brodskius (Markhaseva & Ferrari, 2005).
For Markhaseva, Laakmann & Renz (2014, p.79) the family include only Tharybis Sras, 1902, it is considered to be a true tharybid, but Undinella Sars, 1900 and Brodskius Markhaseva & Ferrari, 2005, conventionally currently remain in the family but are not considered for the family diagnosis. Type genus: Tharybis Sars 1902.
General characters :
1 - Proximal part of right A1 in males with ancestral segments X to XII fused (see Fig. 5).
2 - A2 coxa with or without seta; basis with 2 setae, endopodal segment 1 with 2 setae; setal formula of endopod: 0, 0-0-0, 1, 1, 1, 1, 1, 3 (Table 1).
3 - Md endopodal segment 2 with 9 setae; exopod 5-segmented with 6 setae; gnathobase without hump/crest (see Table 2).
4 - Mx1 setal formula: 13-14, 2-3, 3-4, 2-3, 7 or 9, 3-5, 7 or 9 (see Table 3).
5 - Mx2 endites setal formula: 4, 3, 3, 3, 4; endopod setal formula: 3w + 5br, 3w + 6br, and 3w + 5br + 1sc (see Table 4).
6 - Mxp praecoxal endites: setal formula 1, 2 and 3, with all setae sclerotised (Fig. 6 e), or 1sc + 2sx + (2sx+1w); 1sc + 2sc + (2sc+1br); 1w + (1sc+1w) + (2sc+1w), and 1w + (1sc+1w) + (2sc+1br); basis with 3 prox P5imal and 2 distal nsetae (see Table 5).
7 - Male P5 right basipod large; left P5 biramous, right uniramou, of complex structure (segments of irregular shape); right and left coxa and basis asymmetrical, right significantly shorter than left; right exopod 2-segmented, left 3-segmented (see fig.7 h)
For Markhaseva & al. (2014, p.81) the Tharybidae belong to the ''ancestral'' lineage of ''Bradfordians'' with the most plesiomorphic setation on the Mxp syncoxa praecoxal endites 1, 2, 3 setae. |  Issued from : E.L. Markhaseva, S. Laakmann & J. Renz in Mar. Biodiv., 2014, 44 [p.70, Fig.5]. Schematic view of right A1 in males of ''Bradfordian families. Tharybidae. Roman numerals: ancestral segments; black arrows: fused ancestral segments. |
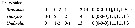 Issued from : E.L. Markhaseva, S. Laakmann & J. Renz in Mar. Biodiv., 2014, 44 [p.73, Table I]. A2 armament (number of seta) in different ''Bradfordian'' genera (females). Tharybidae. c: coxa; b: basis; End 1: endopod segment 1; End 2: endopod segment 2; Exp: exopod. |
 Issued from : E.L. Markhaseva, S. Laakmann & J. Renz in Mar. Biodiv., 2014, 44 [p.74, Table 2]. Md armament (number of seta) in different ''Bradfordian'' genera (females). Tharybidae. b, basis; End 1: endopod segment 1; End 2: endopod segment 2; Exp: exopod; gn: gnathobase. |
 Issued from : E.L. Markhaseva, S. Laakmann & J. Renz in Mar. Biodiv., 2014, 44 [p.76, Table 3]. Mx1 armament (number of seta) in different ''Bradfordian'' genera (females). Tharybidae. pa: praecoxal arthrite (setal formula : terminal+posterior+anterior setae); ce: coxal endite; bp: proximal basal endite; bd: distal basal endite; End: endopod; Exp: exopod; Epi: epipodite. |
 Issued from : E.L. Markhaseva, S. Laakmann & J. Renz in Mar. Biodiv., 2014, 44 [p.78, Table 4]. Mx2 armament (number of seta) in different ''Bradfordian'' genara (females). Tharybidae. at: attenuation; pe: praecoxal endite; ce: coxal endite; bp: proximal basal endite; bd: distal basl endite; el: enditic-like lobe of proximal endopodal segment; End: endopod; w, worm-like seta; br: brush-like seta; sc: sclerotised seta. |
 Issued from : E.L. Markhaseva, S. Laakmann & J. Renz in Mar. Biodiv., 2014, 44 [p.80, Table 5]. Mxp setation (number of seta) in different ''Bradfordian'' genera (females). Tharybidae. at: attenuation; pes: praecoxal endites of syncoxa (from proximal to distal); ces: coxal endite of syncoxa; bp: basis proximal; bd: basis distal; End: endopodal segments 1 to 5. For more detailed morphology of the setae on the praecoxal endites of the Mxp syncoxa see markhaseva & Ferrari (2005) and Markhaseva & al. (2008). |
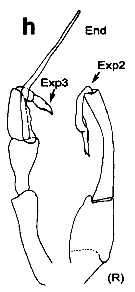 Issued from :E.L. Markhaseva, S. Laakmann & J. Renz in Mar. Biodiv., 2014, 44 [p.72, Fig.7 h]. P5 from Tharybis cf. macrophthalma. R: right leg; Exp: exopod; end: endopod. Markhaseva (pers. obs.). |
 Issued from : G.A. Boxshall & S.H. Halsey in An Introduction to Copepod Diversity. The Ray Society, 2004, No 166, Part. I. [p.209]. Armature formula of swimming legs P1 to P4. |
 Issued from : S. Laakmann, E.L. Markhaseva & J. Renz in Mol. Phylog. Evol., 2019, 130. [p.331, Table 1]. compilation of information on relationships among ''Bradfodian'' genera from Markhaseva & Ferrari 2005) and Markhaseva & al. (2014). Abbreviations: A2, antenna; Md, mandible; Mx1, maxillule; Mx2, maxilla; Mxp, maxilliped ; P5, leg 5. w, worm-like sensory seta; b, brush-like sensory seta; s, sclerotized seta.; | | | | | (*) Cenognatha Bradford-Grieve, 2001 | |
| | Ref.: | Bradford-Grieve, 2001 a (p.792); Bradford-Grieve, 2004 (p.287) | | Rem.: | type: Neoscolecithrix antarctica. 1 sp. (provisionally). Bradford-Grieve, 2004 (p.285) includes in this genus the two species Neoscolecithrix caetanoi and N. farrani. Boxshall & Halsey, 2004 (p.186). Cf. Scolecitrichidae (largo sensu). | | | | (*) Neoscolecithrix Canu, 1896 (part.) | |
| | Syn.: | Oothrix Farran, 1905 (p.42); van Breemen, 1908 a (p.67); Rose, 1933 a (p.140) | | Ref.: | Brodsky, 1950 (1967) (p.225); Fosshagen, 1972 a (p.1); Bradford, 1973 (p.147, 149, Rem.); Razouls, 1982 (p.369); Bradford & al., 1983 (Déf., p.123); Hulsemann, 1985 a (p.55, Rem.: 2 groupes); Alvarez, 1985 a (p.197, Rev., 2 groupes: 'koehleri', 'farrani' ); Razouls, 1993 (p.311); Mauchline, 1998 (p.90: M); Vyshkvartzeva, 1999 (2000) (p.217-218); Bradford-Grieve, 2001 a (p.781, 791, Def.); Bradford-Grieve, 2004 (p.287); Boxshall & Halsey, 2004 (p.185, 210: Rem.) | | Rem.: | type: Neoscolecithrix koehleri Canu,1896. Ohtsuka, Boxshall & Fosshagen (2003, p.61-62) believe that this genus belongs (largo sensu) to Scolecitrichidae. | | | | Paratharybis Tanaka, 1937 | |
| | Ref.: | Tanaka, 1937 (p.264); Vervoort, 1957 (p.96, Rem.) | | Rem.: | Cf. Undinella | | | | (1) Parundinella Fleminger, 1957 | |
| | Ref.: | Fleminger, 1957 a (p.348); Bradford, 1973 (p.147); Schulz, 1981 (p.169); Razouls, 1982 (p.370, 384); Bradford & al., 1983 (p.123, Def.); Razouls, 1993 (p.311); Mauchline, 1998 (p.82, 90: M; p.84, 87: F); Andronov, 2002 (p.3, 26, clé des spp.); Bradford-Grieve, 2004 (p.287); Ohtsuka & al., 2003 (p.62: Rem.); Boxshall & Halsey, 2004 (p.210); Markhaseva & Renz, 2011 (p.67, Rem.); Markhaseva & al., 2013 (p.22, Table 1, 2, 3, 4, Rem.: p.84: p.19); Laakmann & al., 2019 (p.330, Table 1: considered as incertae sedis genera) | | Rem.: | Total 4 spp.
Diagnosis after Bradford, Haakonssen & Jillett (1983, p.124), after Fleminger 1957 a :
- Head and pediger segment 1 fused, 4th and 5th pediger segments fused.
- Posterolateral corners of metasome produced into lobiform or spiniform process.
- Genital segment symmetrical, swollen laterally, ventrally only weakly produced.
- Rostrum simple, bifurcate, with slender filament on each side.
- A1 23-segmented in female, 21-segmented in male.
- Md blade elongate with 3 to 4 monocuspid, spiniform teeth confined to dorsal-most portion of lobe.
- Mx1 inner lobe 1 moderately sized, not broad or truncate.
Mx2 lobe 5 with 2 sensory filaments, 1 normal seta and 1 enlarged falcate seta; terminal part of endopod with 5 or 6 sensory filaments, some with apical flagellum.
- External exopod spines of P2-P4 ornamented with small denticles along upper and lower margins.
- Female P5 minute, 1-segmented, attached to common basal segment; distal segment terminated by 1 or more pointed processes and 1 robust inner edge spine bearing ventral spinules.
Male P5 biramous, asymmetrical; left leg exopod 3-segmented, segment 1 with inner proximal process, endopod 1- or 2-segmented; right leg exopod 2-segmented, endopod in part fused with basipod segment 2.
For Markhaseva, Laakmann & Renz (2014, p.84) this genus must be placed outside Tharybidae, his status remains taxonomically unresolved. Fleminger's description is not detailed enough to clarify the position of Parundinella within the ''Bradfordians''. Several characters exclude this genus apart from the Tharybidae: 1 - A2 endopodal segment 1 with 1 seta (versus 2 setae in Tharybis and exopod armament as 0, 0-1-1-1, 1, 1, 1, 0, 3 (versus 0, 0-0-0, 1, 1, 1, 1, 1, 3 in Tharybis); 2 - Mx1 praecoxal arthrite with 10-12 setal elements (versus 13-14 in Tharybis), exopod with 7 setae (versus 3-5 setae in Tharybis); 3 - Mx2 endopod with 5-6 setal elements (versus 8-9 setae in Tharybis); 4 - Mxp praecoxal lobes with a setal formula as 1, 2 and 2? (versus 1, 2 and 3 setae in Tharybis) (see Table 1-5); 5 - male P5, right and left coxa and basis of nearly same length (versus right and left basipods significantly asymmetrical in Tharybis), P5 right leg biramous (versus uniramous in Tharybis). | | Remarks on dimensions and sex ratio: | | The mean female size is 0.868 mm (n = 5; SD = 0.0760), and the mean male size is 0.810 mm (n = 4; SD = 0.0529). The size ratio (Male: Female) is comprised between 0.892 and 0.933. | | | | | Pseudophaenna Sars, 1902 | | Ref.: | Sars,1902 (1903) (p.43); van Breemen, 1908 a (p.57); Rose, 1933 a (p.126); Bradford, 1973 (p.138, Rem.); Razouls, 1982 (p.287, 368); Bradford & al., 1983 (p.123, Déf., p.126); Razouls, 1993 (p.311); Vyshkvartzeva, 2001 (p.77: Rem.); Bradford-Grieve, 2004 (p.287) | | Rem.: | Boxshall & Halsey (2004, p.96) transfer this genus to the Diaixidae family. | | | | (*) Rythabis Schulz, 1995 | |
| | Ref.: | in Schulz & Beckmann, 1995 (p.199); Mauchline, 1998 (p.84: F); Ohtsuka & al., 2003 (p.61-62: Rem.); Bradford-Grieve, 2004 (p.287); Boxshall & Halsey, 2004 (p.185, 186) | | Rem.: | Cf. Scolecitrichidae | | | | | Ref.: | Sars, 1902 (1903) (p.67); van Breemen, 1908 a (p.86); Rose, 1933 a (p.164); Tanaka, 1960 a (p.127); Andronov, 1976 (p.1903); Schulz, 1981 (p.170, Rev.); Razouls, 1982 (p.383); Gardner & Szabo, 1982 (p.309); Bradford & al., 1983 (p.123 : Rem, 126, Def.,); Razouls, 1993 (p.311); Mauchline, 1998 (p.81, 90: M; p.84, 87: F); Bradford-Grieve & al., 1999 (p.935: spp. Key); Andronov, 2002 (p.3, clé des spp.); Ohtsuka & al., 2003 (p.62: Rem.); Bradford-Grieve, 2004 (p.287); Ferrari & Markhaseva, 2005 (p.33, Rem.: p.45); Markhaseva & Ferrari, 2005 a (p.111, Fig.31, Rem.); Boxshall & Halsey, 2004 (p.210); Vives & Shmeleva, 2007 (p.858, spp. Key); Markhaseva & Renz, 2011 (p.67, 68, Rem.); Renz & Markhaseva, 2015 (p.96, Table 4, Fig.3, sex ratio, biogeography); Laakmann & al., 2019 (p.660, Table 1). | | Rem.: | type: Tharybis macrophthalma Sars, 1903. Total: 22 spp.
Diagnosis from Bradford, Haakonssen & Jillett (1983, p.126), after Schulz, 1981 :
- Head and pediger segment 1 fused or separate, pediger segments 4 and 5 fused.
- Rostrum short and rounded with or without 2 filaments.
- A1 24-segmented in female, 22-segmented on right and 23-segmented on left in male.
- A2 exopod more than twice as long as endopod.
- Md blade with 2 unusually strong bifid teeth followed by dense series of plumose setae; palp with both rami well developed.
- Mx1 with inner lobe 1 enlarged, extending beyond remaider of appendage; exopod reduced with 3 to 5 setae.
- Mx2 endopod with 3 (4?) worm-like and 6 (4,) brush-like sensory filaments; lobes extend over more than half appendage.
-Mxp basipod swollen;
- Posterior surface of swimming legs may bear small spinules,
- Terminal spine of P2-P4 coarsely serrated.
- Female P5 of two segments attached to common basal segment, terminal segment longest; terminal segment with 1 or 2 terminal spines as well as articulated inner edge spine.
- Male P5 asymmetrical, usually biramous on left, uniramous on right; left leg with 2 basal segments, exopod 3-segmented, shorter than the one-segmented endopod, segment 3 inserted terminally; right leg 3-segmented, segment 2 with inner edge distal process.
Remarks: Tharybis and Undinella are difficult to separate when all their species are taken into account. | | Remarks on dimensions and sex ratio: | | The mean female size is 1.286 mm (n = 21; SD = 0.1712), and the mean male size is 1.172 mm (n = 17; SD = 0.2169). The size ratio (Male: Female) is 0.890 (n = 15; SD = 0.0713). The sex ratio (female: male) is probably 1 in the genus. | | | | | | Syn.: | Paratharybis Tanaka, 1937 | | Ref.: | Sars, 1900 (p.51); van Breemen, 1908 a (p.67); Rose, 1933 a (p.142); Brodsky, 1950 (1967) (p.276); Vervoort, 1957 (p.96, Rem.); Tanaka, 1960 a (p.129); Andronov, 1976 (p.1903); Schulz, 1981 (p.169); Razouls, 1982 (p.380); Bradford & al., 1983 (Rem.: p.123, 127: Def.); Razouls, 1993 (p.311); Chihara & Murano, 1997 (p.920, figs.F,M); Mauchline, 1998 (p.87: F; p.90, 93: M); Andronov, 2002 (p.7, 62, spp. Key); Ohtsuka & al., 2003 (p.62: Rem.); Bradford-Grieve, 2004 (p.287); Boxshall & Halsey, 2004 (p.210); Markhaseva & Ferrari, 2005a (p.11, fig.31, Rem.); Vives & Shmeleva, 2007 (p.864, spp. Key); Markhaseva & Renz, 2011 (p.67, Rem.); Laakmann & al., 2019 (p.330, Table 1) | | Rem.: | type: Undinella oblonga Sars,1900. Total: 9 spp. + 1 undet.
Diagnosis from Bradford, Haakonssen & Jillett (1983, p.127), after Sars, 1900 and Fleminger, 1957 :
- Head and pediger segment 1 partly separate, pediger segments 4 and 5 fused or separate.
- Posterior corners of metasome prolonged posteriorly in female.
- Rostrum with basal portion bifid, both parts terminated by 1 filament.
- A1 24-segmented in female; 23-segmented in male.
- A2 exopod more than twice as long as endopod.
- Md blade with 2 strong bidentate teeth; palp with endopod larger than exopod.
- Mx1 inner lobe 1 moderately enlarged, not extending beyond endopod; exopod reduced, with 2 or 3 setae.
- Mx2 endopod with sensory filaments; lobes crowded on distal half of appendage.
- Mxp slender.
- Posterior surfaces of swimming legs may have some small spinules.
- Terminal spine of P2-P4 with fine shallow serrations.
- Female P5 symmetrical or asymmetrical, 2-segmented, attached to common basal segment; segments of approximately equal length; distal segment with 2 to 4 short terminal spines and sometimes outer edge spine.
- Male P5 asymmetrical; uniramous on right, 3-segmented, segment 2 usually with inner edge distal process; biramous on left, with on, endopod 1-segmented, longer than 3-segmented exopod, exopod segment 3 inserted subterminally on segment 2 to make pincers. basal segment attached to common basal segment.
Remarks: Tharybis and Undinella are difficult to separate when all their species are taken into account. | | Remarks on dimensions and sex ratio: | | The mean female size is 2.071 mm (n = 16; SD = 0.5889), and the mean male size is 1.719 mm (n = 15; SD = 0.1628). The size ratio (Male: Female) is 0.880 (n = 8; SD = 0.0880). The sex ratio (female: male) is probably 1. | | | | (4) incertae sedis (Tharybidae) | |
| | Rem.: | The following species would belong to this family:
[1] "Amallothrix" robustipes Grice & Hulsemann,1965 (F)
Syn.: ? Xanthocalanus paululus Park, 1970 (p.497); Roe, 1975 (p.364)
Ref.: Grice & Hulsemann, 1965 (p.239, Descr.F, figs.F); 1967 (p.16); Bradford, 1973 (p.147, Rem.); Roe, 1975 (p.365, Rem.); Bradford & al., 1983 (p.123, Rem.)
Loc.: Atlant. NE (off Canaries-Açores-), ? Is. du Cap Vert, ? G. du Mexique, Indien W
N: 2
Lg.: (226) F: 1,13; {F: 1,13}
Xanthocalanus groenlandicus Tupitzky,1982 (F,M)
Ref.: Tupitzky, 1982 (p.297, figs.F,M); Kosobokova & al., 1955 (p.194)
Loc.: Arct., mer de Laptev
Lg.: (453) F: 1,5-1,4; M: 1,4; {F: 1,40-1,50; M: 1,40}
Rem.: Campaner, 1983 (comm. pers.): Cf. ? Tharybis. Voir spp. inc. sedis
[2] "Xanthocalanus" hispidus Grice & Hulsemann, 1967 (F) [Figs] details 
Xanthocalanus macrocephalon Grice & Hulsemann,1970 (F)
Ref.: Grice & Hulsemann, 1970 (p.191, Descr.F, figs.F); Bradford, 1973 (p.139, 147, Rem.); Bradford & al., 1983 (p.127); Schulz & Beckmann, 1995 (p.210, Rem.)
Loc.: off Woods Hole
N: 1
Lg.: (200) F: 1,12-1,06; {F: 1,06-1,12}
Rem.: Cf. Tharybis
Xanthocalanus paraincertus Grice & Hulsemann,1965 (F)
Ref.: Grice & Hulsemann, 1965 (part., p.235, Descr.F, figs.F); Bradford, 1973 (p.139, 147, Rem.); Bradford & al., 1983 (p.127, Rem.); Schulz & Beckmann, 1995 (p.210, Rem.)
Loc.: Atlant. NE (locality not specified)
N: 1
Lg.: (226) F: 1,61-1,15; {F: 1,15-1,61}
Rem.: abyssopelagic. Cf. Tharybis
“Xanthocalanus” paululus Park,1970 (F,M)
Ref.: Park, 1970 (p.497, Descr.F, figs.F); Bradford, 1973 (p.139, 147, Rem.); Roe, 1975 (p.364, Descr.F,M, figs.F,M, Rem.); Bradford, 1983 (p.127, Rem.)
Ref. compl.: Suarez-Morales & Gasca, 1998 a (p.110)
Loc.: Is. du Cap Vert, Mer des Caraïbes, G. du Mexique
N: 3
Lg.: (8) F: 1,29-1,14; M: 1,37-1,29; (88) F: 1,28-1,22; {F: 1,14-1,29; M: 1,29-1,37}
Rem.: No “Xanthocalanus” hispidus. ? Cf. Undinella. Cf.: Brodskius paululus
| | | | | |
|
|
 Any use of this site for a publication will be mentioned with the following reference : Any use of this site for a publication will be mentioned with the following reference :
Razouls C., Desreumaux N., Kouwenberg J. and de Bovée F., 2005-2026. - Biodiversity of Marine Planktonic Copepods (morphology, geographical distribution and biological data). Sorbonne University, CNRS. Available at http://copepodes.obs-banyuls.fr/en [Accessed February 01, 2026] © copyright 2005-2026 Sorbonne University, CNRS
|
|
 |
 |





